 |
The methodology used to evaluate the safety performance of improved traffic signal conspicuity is based on the application of an auto-insurance claim prediction model. A claim prediction model is mathematical model that relates the claim frequency experienced by a road entity (intersection, road segment, etc.) to the various traffic and geometric characteristics of that entity. Prediction models that are developed on collision records are more common in the road safety engineering literature, however, in British Columbia the reliability of collision records have deteriorated and as such, alternate road safety data (i.e., claims data) can be used. Collision or claim models have several road safety engineering applications such as the evaluation of the safety for various road facilities, identifying problematic locations, and evaluating the effectiveness of road safety improvement measures.
In general, there are two main approaches that can be used to model road safety. The first option is to use conventional linear regression, whereas the second option is to use a generalized linear modeling approach (GLIM). Conventional linear regression assumes a Normal distribution error structure whereas a generalized linear modeling approach (GLIM) assumes a non-Normal distribution error structure (usually Poisson or negative binomial). In the past, many researchers developed collision prediction models using conventional linear regression. However, several researchers (Jovanis and Chang, 1986, Hauer et-al., 1988) have shown that conventional linear regression models lack the distributional property to adequately describe collisions. This inadequacy is due to the random, discrete, non-negative, and typically sporadic nature that characterize the occurrence of a vehicle collision (these characteristics also describe an auto insurance claim). GLIM has the advantage of overcoming these shortcomings of conventional linear regression and recognizing these advantages, the GLIM approach was utilized in this study.
The theoretical background concerning the development of these prediction models is beyond the scope of this paper and the reader is directed to road safety engineering literature for more information.
The prediction model structure relates the frequency of auto insurance claims to the product of traffic flows entering the intersection. In some cases, the sum of the traffic flows entering the intersection is used instead of the product of the traffic flows. However, it is has been shown (Hauer, 1988) that a model that utilizes the product of the traffic flows, provides a better representation of the relationships between collisions (or claims) and the traffic flows at intersections. In this model structure, claim frequency is a function of the product of traffic flows raised to a specific power (usually less than one). The model form is shown below in equation (1).
(Equation 1)
![]()
where:
E(Λ) = expected auto insurance claim frequency,
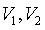 = major / minor road traffic
volume (AADT),
= major / minor road traffic
volume (AADT),
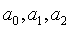 = model parameters.
= model parameters.
The claim prediction model that used for the analysis of the signal head effectiveness is based on the work of Sayed and de Leur (de Leur and Sayed, 2001). The developed claim prediction model is assumed to follow a negative binomial distribution that is included within the GLIM software package through a macro designed by NAG (NAG, 1996). The model predicts the total number of claims over a three-year time period at a signalized intersection based on major and minor road traffic volumes. The prediction model and the model parameters are shown in Table 1.
Table 1: Developed Claim Prediction Models
| Model Formulation | t-ratio | S.D. (DoF) | Pearson x2 (x2 test) |
||
|---|---|---|---|---|---|
MODEL
1: Total Claims Model: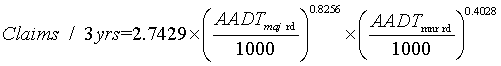 |
A0 A1 A2 |
2.3 6.8 4.3 |
5.36 |
113 (105) |
101 (129) |
Several measures are used
to assess the significance of GLIM models. These measures include the t-ratio
test for the model parameters, the ![]() value (the model’s dispersion parameter), the scaled deviance (SD), and the
Pearson x2 statistic. The SD is defined as the likelihood
test ratios, measuring the difference between the log likelihood of the model
and the saturated model (Kulmala, 1995). The formulation of SD (for a negative
binomial distribution) is shown in equation (2). The Pearson x2 statistic is another measure to assess the significance of a GLIM model and
is shown in equation (3). For a well-fitted model, both the scaled deviance
and the Pearson x2 should be significant compared with the
value obtained from the x2 table for the given degrees of
freedom.
value (the model’s dispersion parameter), the scaled deviance (SD), and the
Pearson x2 statistic. The SD is defined as the likelihood
test ratios, measuring the difference between the log likelihood of the model
and the saturated model (Kulmala, 1995). The formulation of SD (for a negative
binomial distribution) is shown in equation (2). The Pearson x2 statistic is another measure to assess the significance of a GLIM model and
is shown in equation (3). For a well-fitted model, both the scaled deviance
and the Pearson x2 should be significant compared with the
value obtained from the x2 table for the given degrees of
freedom.
(Equation 2)
![Equation 2: SD = 2\sum\limits_{i = 1}^n {\left[ {y_i \ln \left( {{{y_i } \over {E\left( {\Lambda _i } \right)}}} \right) - (y_i + \kappa )\ln \left( {{{y_i + \kappa } \over {E\left( {\Lambda _i } \right) + \kappa }}} \right)} \right]}](eq2.gif)
where:
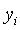 = observed number of claims
at an intersection,
= observed number of claims
at an intersection,
![]() = predicted number of claims obtained from model,
= predicted number of claims obtained from model,
![]() =
shape parameter of the distribution and the mean
=
shape parameter of the distribution and the mean
(Equation 3)
![Equation 3: {\rm{Pearson }}x^2 = \sum\limits_{i = 1}^n {{{\left[ {y_i - E\left( {\Lambda _i } \right)} \right]^2 } \over {Var\left( {y_i } \right)}}}](eq3.gif)
where:
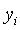 = observed number of claims
at an intersection,
= observed number of claims
at an intersection,
![]() = predicted number of claims obtained from model,
= predicted number of claims obtained from model,
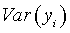 = the
variance of the observed claims.
= the
variance of the observed claims.
These measures indicate that the claim prediction model that is to be used for this analysis has a relatively good fit and the value that is calculated for the t-ratios for all independent variables are significant.
|
United States Department of Transportation - Federal Highway Administration |
||