|
|
2009 Edition Part 2 Figure 2D-15. Examples of Multi-Lane Crossroad Signing for a Cloverleaf Interchange
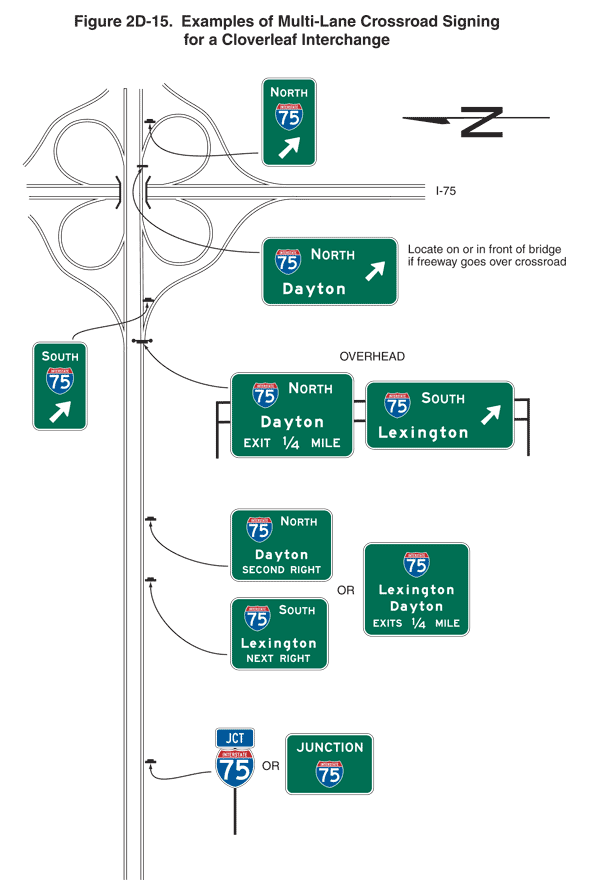
Figure 2D-15. Examples of Multi-Lane Crossroad Signing for a Cloverleaf Interchange
This figure shows examples of multi-lane crossroad signing for a cloverleaf interchange.
The figure shows two highways, an unnamed highway running vertically and I-75 running horizontally. The interchange between the two is shown as a cloverleaf. At the top right of the figure, a black capital letter "N" is shown superimposed on a left-pointing horizontal black arrow, denoting the compass direction.
A series of signs and sign assemblies are shown for one direction of travel along the vertical highway from the bottom to the top of the figure. Except as otherwise noted, all signs and sign assemblies are horizontal rectangular green signs with white borders and lettering.
This figure shows eight signs and sign assemblies along the vertical highway:
- At the bottom of the figure, a pair of signs are shown to the right of the highway separated by the word "OR." The left sign is shown as a red and blue Interstate shield for I-75. Above it, a plaque is shown with the word "JCT" in white letters and a white border on a blue background. The right sign is shown as a horizontal rectangular sign with the word "JUNCTION" on the top line and the Interstate shield for I-75 on the bottom line.
- Closer to the interchange, the second sign is shown to the right of the highway. It shows the Interstate shield for I-75 to the left of the word "SOUTH" on the top line, the word "Lexington" on the middle line, and the words "NEXT RIGHT" on the bottom line.
- The third sign is shown with the same I-75 shield on the top line to the left of the word "NORTH" on the top line, the word "Dayton" on the middle line, and the words "SECOND RIGHT" on the bottom line. To the right of the second and third sign is the word "OR" and another sign. It is shown with an I-75 shield on the top line, the word "Lexington" on the second line, the word "Dayton" on the third line, and the words "EXITS 1/4 MILE" on the fourth line.
- Just prior to the first right entrance ramp, the fourth and fifth signs are shown as located over the highway. The two signs are shown in a horizontal array superimposed on two horizontal black lines between two short vertical black lines. The word "OVERHEAD" is shown above them. The left sign shows an Interstate shield for I-75 to the left of the word "NORTH" on the top line, the word "Dayton" on the middle line, and the words "EXIT 1/4 MILE" on the bottom line. The right sign shows an Interstate shield for I-75 to the left of the word "SOUTH" on the top line and the word "Lexington" on the bottom line. A short diagonal arrow pointing up and to the right is shown to the right of and slightly above the word "Lexington."
- The sixth sign is shown in the gore between the right lane of the vertical highway and the first right entrance to I-75. It is shown as a vertical rectangular green sign with a white border and legend. The word "SOUTH" is shown on the top line, an Interstate shield for I-75 is shown on the middle line, and a short diagonal arrow pointing up and to the right is shown on the bottom line.
- Near the top of the figure, the seventh sign is shown located just beyond the horizontal highway just prior to the second right entrance ramp. An Interstate shield for I-75 is shown to the left of the word "NORTH" on the top line. The word "Dayton" is shown on the bottom line. A short diagonal arrow pointing up and to the right is shown to the right of and slightly above the word "Dayton." To the right of the sign are the words "Locate on or in front of bridge if freeway goes over crossroad."
- The eighth sign is shown just beyond the second right entrance ramp and is located in the gore between the right lane of the vertical highway and the right entrance ramp. It is shown as a vertical rectangular green sign with a white border and legend. The word "SOUTH" is shown on the top line, an Interstate shield for I-75 is shown on the middle line, and a short diagonal arrow pointing up and to the right is shown on the bottom line.
